INT vs FP Data Types for Quantization
The Weekly Salt #94
This week, we review:
⭐Data-Efficient RLVR via Off-Policy Influence Guidance
INT v.s. FP: A Comprehensive Study of Fine-Grained Low-bit Quantization Formats
Parallel Loop Transformer for Efficient Test-Time Computation Scaling
⭐Data-Efficient RLVR via Off-Policy Influence Guidance
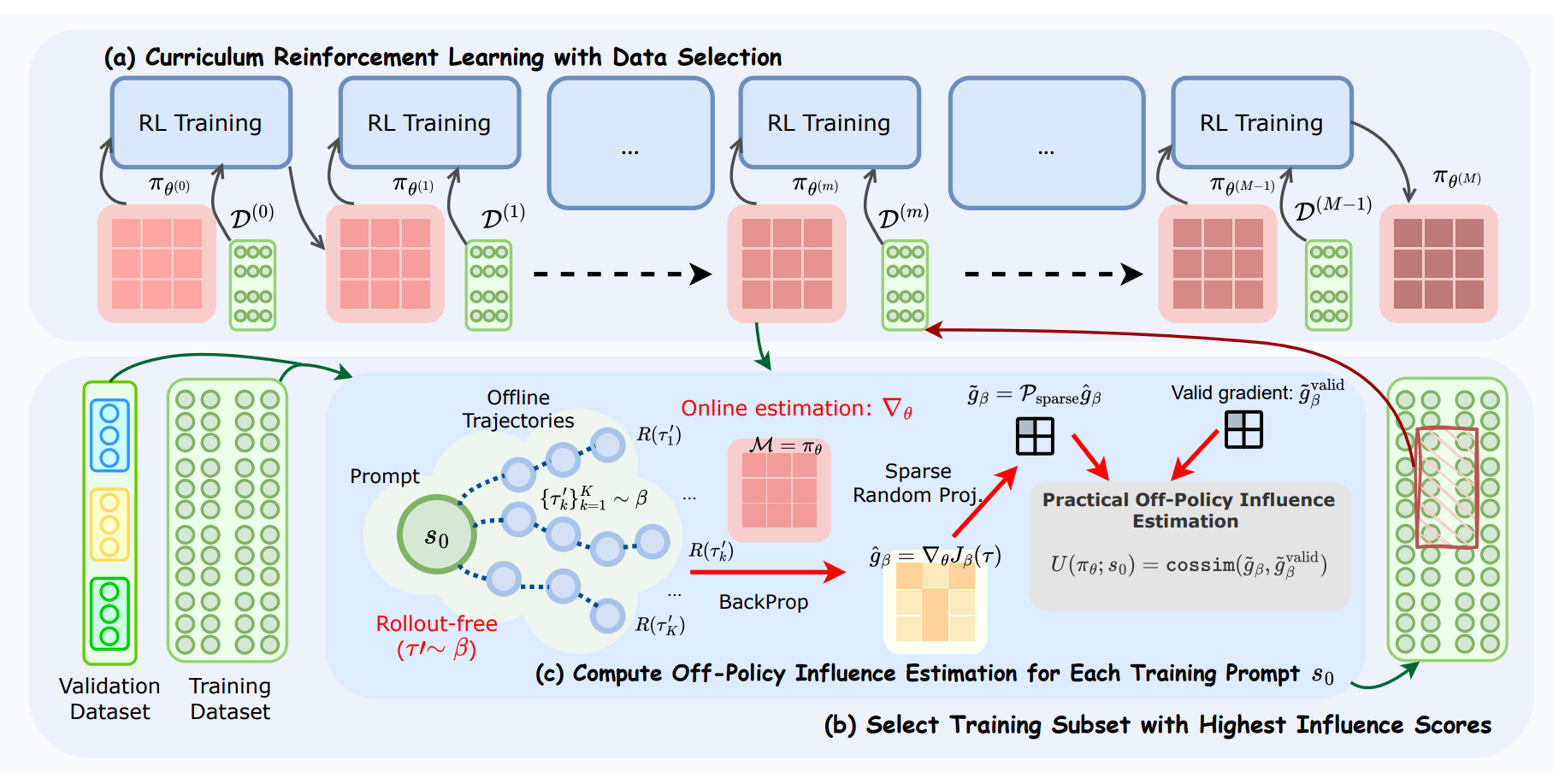
Reinforcement learning (RL) for reasoning-heavy LLMs keeps running into the same brick wall: we waste a lot of rollouts on the wrong training prompts.
This paper argues that the right fix isn’t another heuristic notion of “hardness,” but a principled measure of how much each prompt actually moves the current policy. The core move is to import influence functions into RLVR and compute a per-prompt influence score from gradients, then use those scores to drive data selection. The catch, of course, is that on-policy gradients are expensive to get in RL.
The authors’ answer is off-policy influence estimation: reuse pre-collected trajectories to approximate the gradient for any candidate prompt and sidestep fresh rollouts during selection.
Two pragmatic details make this workable at LLM scale. First, they compress gradients via sparse random projection to keep storage and dot products cheap, and they add dropout before projection to better preserve inner products after compression. Second, they wrap the whole thing in a multi-stage curriculum, CROPI, where each stage selects the currently most influential prompts for the next chunk of RL updates. This shifts data selection from static filtering to a dynamic, checkpoint-conditioned loop that tracks the policy as it changes.
Does off-policy influence faithfully reflect on-policy learning?
The paper did some sanity checks. Using a small suite of problems, the cosine similarity between off-policy and on-policy gradients exceeds 0.6 for 40 out of 50 pairs, good enough to rank prompts most of the time, not good enough to stop worrying.
Rank preservation improves sharply once the projection gets even mildly dense (sparsity ≈0.9), which supports the “dropout then project” trick. Still, this is an estimator built from yesterday’s trajectories, so it will miss shifts in exploration and any reward-model quirks that only show up on fresh rollouts.
INT v.s. FP: A Comprehensive Study of Fine-Grained Low-bit Quantization Formats
The paper challenges the prevailing push toward low-precision floating point for LLMs by showing a clean crossover: coarse granularity favors FP, but at fine granularity (block-wise) well-designed INT wins more often than not.
In particular, MXINT8 consistently beats MXFP8 on accuracy while also being cheaper in area and energy. For 4-bit, FP keeps an edge on average, yet the gap narrows, and with a simple outlier mitigation (random Hadamard rotation), NVINT4 can surpass NVFP4. The overall message is pragmatic: format choice should follow granularity and bit-width, not marketing slogans.
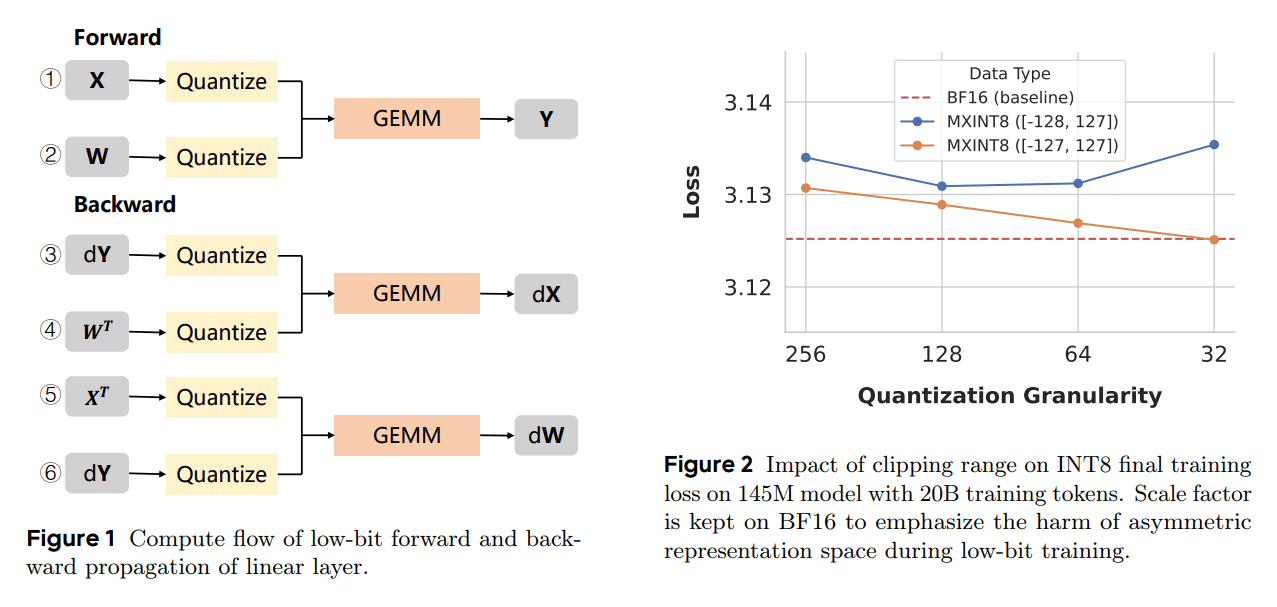
The authors analyze quantization for both families and show how smaller blocks reduce local dynamic range, which favors the uniform density of INT.
A symmetric clipping rule removes the small but consequential bias that INT can introduce during backprop at fine granularity. They also highlight a pitfall in using BF16 to compute INT scales: a non-trivial fraction of values mis-map to −128 without a forced symmetric clamp.
In their experiments, MXINT8 beats MXFP8 on every model. With Hadamard rotation, NVINT4 and MXINT8 sweep all models against their FP peers.
Training tells a similar story. On 1B and 3B Llama3-style models trained for 100B/200B tokens, MXINT8 tracks BF16 almost perfectly and slightly outperforms MXFP8 in loss by ~1e-3 while matching downstream task accuracy. That finding matters because it pushes back on the idea that “only FP8 trains well”; with the right clipping and scaling, INT8 training is essentially lossless and operationally straightforward.
Parallel Loop Transformer for Efficient Test-Time Computation Scaling
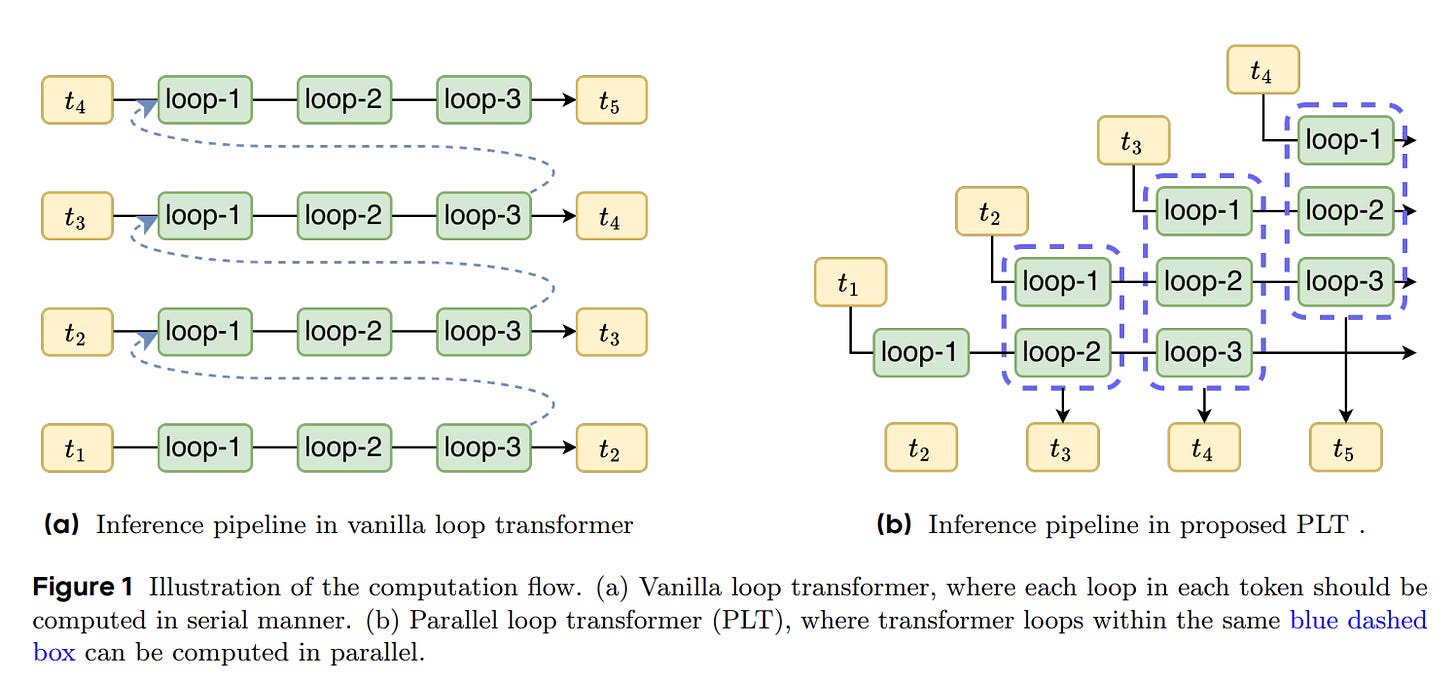
The paper proposes the Parallel Loop Transformer (PLT): a looped-transformer variant that keeps the parameter-efficiency of weight sharing while sidestepping the usual O(L) latency penalty at inference.
The key idea is to parallelize across loops and tokens so effective depth scales without serializing compute.
It proposes a cross-loop parallelism (CLP), which schedules different loop iterations on adjacent tokens within a single forward pass, and an “efficient representation enhancement” that avoids ballooning the KV cache by sharing the first loop’s cache and fusing it with a local sliding-window path. In short, PLT tries to get most of the depth benefit of looping at near-vanilla latency and memory.
Mechanically, CLP executes the l-th loop on token i alongside the (l+1)-th loop on token i−1, collapsing L sequential steps into one pass during decoding. To keep memory bounded, later loops reuse K/V from loop-1, then add a gated sliding-window attention (window size 64 in experiments) so later loops still capture local context that isn’t in the shared cache. The result is a single global KV footprint plus a small per-loop window, with the gate blending global and local signals per head. Training mirrors this structure without cross-token activation dependencies, so the inference schedule is feasible without architectural contortions.
On an in-house 680M-activated/13B-total MoE baseline (“Seed-MoE”), the ablation table is convincing: naïvely adding two loops boosts accuracy but doubles latency and KV memory, while adding CLP recovers most of the latency (from ~9.4 ms to ~5.9 ms at bs=4) and preserves accuracy.