Pre-Training Updates: NVFP4 and Thinking Augmented
The Weekly Salt #89
This week, we review:
⭐Random Policy Valuation is Enough for LLM Reasoning with Verifiable Rewards
Pretraining Large Language Models with NVFP4
Thinking Augmented Pre-training
⭐Random Policy Valuation is Enough for LLM Reasoning with Verifiable Rewards
The paper argues that many recent “RL with Verifiable Rewards” (RLVR) pipelines for LLM math reasoning are over-engineered.
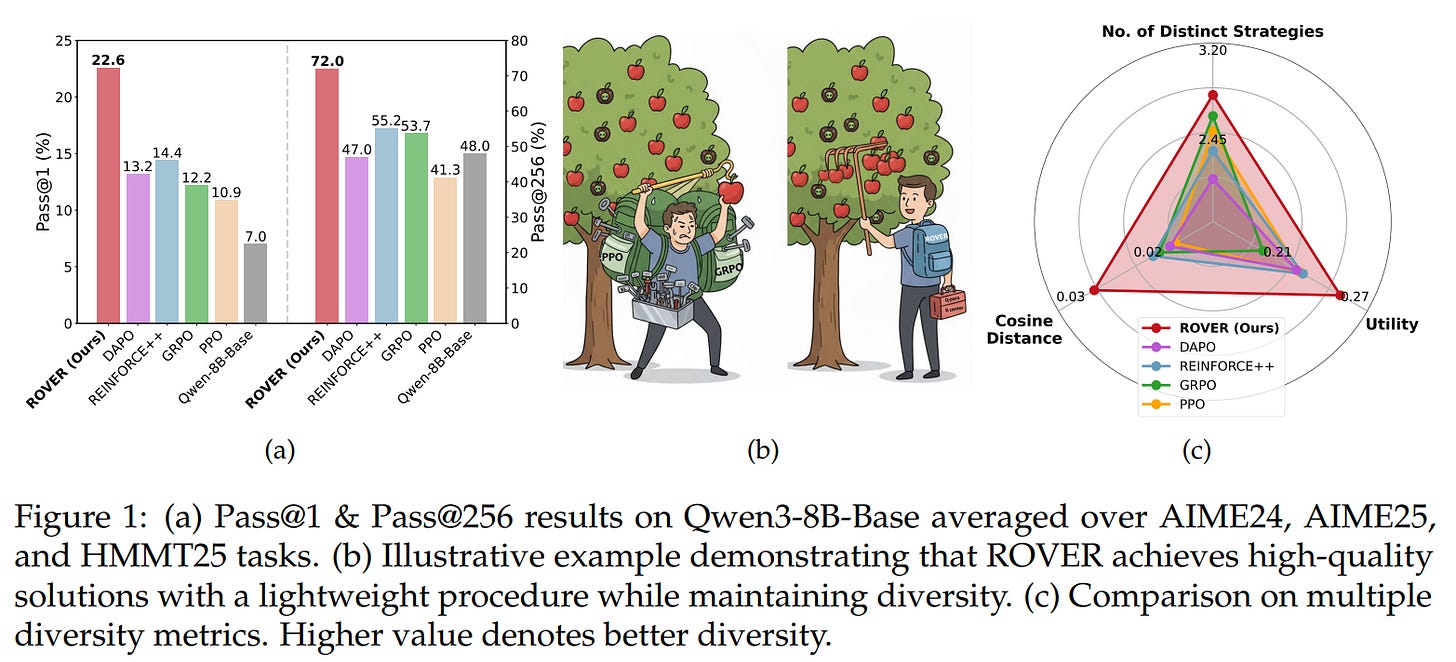
The authors model RLVR as a finite-horizon Markov Decision (MDP) Process whose states evolve deterministically along a tree of intermediate reasoning steps and yield binary terminal rewards when a verifier checks the final answer. In this setting, they prove a striking result: you don’t need the usual generalized policy iteration loop (e.g., PPO/GRPO). Instead, the optimal next action can be identified directly from the Q-function of a fixed uniformly random policy, which neatly sidesteps instability, collapse of solution diversity, and the assortment of heuristics that policy-optimization methods typically require.
Building on this, they introduce ROVER (Random pOlicy Valuation for divERse reasoning), a minimalist training scheme that evaluates Q-values under the random policy and then samples actions via a softmax over those Q-values.
Because it never chases its own policy, ROVER maintains exploration of multiple reasoning branches and avoids the feedback loops that can prune diversity. Across standard math benchmarks and multiple base models, ROVER reports notable gains in both solution quality (e.g., +8.2 pass@1 and +16.8 pass@256) and diversity (+17.6%), despite being far simpler than strong PPO/GRPO baselines.
If you’re thinking about trying this line of work yourself, a few quick pointers:
Treat verifier-checked math as a deterministic tree MDP; exploit that structure rather than importing generic RL tricks.
Start with random-policy Q estimation and softmax action sampling to preserve branch diversity.
Instrument both correctness metrics (pass@k) and path diversity during training; the latter is a first-class objective here.
The authors released their code here:
GitHub: tinnerhrhe/ROVER/
Pretraining Large Language Models with NVFP4
The paper presents a path to stable 4-bit pretraining of LLMs using NVIDIA’s NVFP4 microscaling format. I have evaluated NVFP4 for post-training quantization, and it works quite well. It doesn't reach SOTA accuracy but makes inference >2x faster thanks to Blackwell’s hardware acceleration for NVFP4.
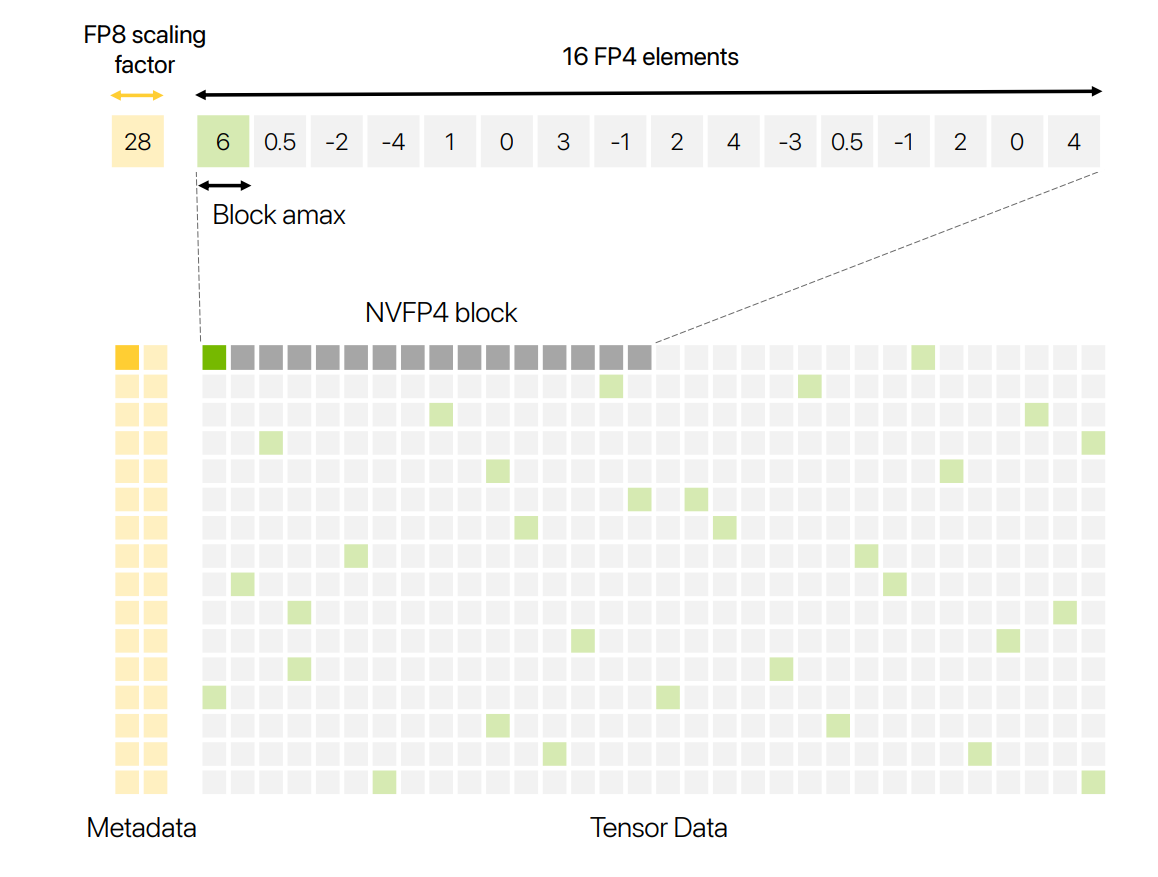
NVFP4 shrinks block size to 16 elements and stores block scales in E4M3 (with an extra FP32 tensor-level scale), improving local dynamic range versus MXFP4 and mitigating FP4 saturation/underflow. On Blackwell Tensor Cores, FP4 math reaches ~2–3× FP8 throughput with ~½ the memory, making the case that, if accuracy holds, FP4 can materially cut training cost.
Accuracy hinges on a training recipe: (1) 2D block scaling to keep forward/backward quantization consistent, (2) Random Hadamard Transforms (RHT) to disperse outliers, (3) stochastic rounding on gradients (not activations/weights) to remove quantization bias, and (4) a few selective high-precision layers. Ablations indicate RHT improves loss while Fprop/Dgrad transforms bring little or no gain.
Empirically, they pretrain a 12B hybrid Mamba-Transformer for 10T tokens, to the authors’ knowledge, the longest publicly documented FP4 run, and match an FP8 baseline closely: e.g., MMLU-Pro 5-shot 62.58 (NVFP4) vs 62.62 (FP8), with broadly comparable results across general, math, multilingual, and commonsense suites (some wins, some small regressions). The loss curve tracks FP8 through a long horizon, underscoring that the method scales beyond toy settings.
Thinking Augmented Pre-training
The paper proposes Thinking Augmented Pre-training (TPT): expand ordinary pre-training text by appending an automatically generated “thinking trajectory” that decomposes the hard parts of the passage, so high-value tokens become easier to learn. The authors run this at scale, up to 100B training tokens, and claim efficiency gains: ~3× better data efficiency overall and >10% post-training improvement on several reasoning benchmarks for a 3B-param model. The intuition is straightforward: when the rationale behind a single answer token is deep, exposing the steps during training lets smaller models internalize it without brittle memorization.
Mechanically, TPT is intentionally simple and “pipeline-friendly”: (1) generate a thinking trajectory for each document using an off-the-shelf LLM with a fixed prompt; (2) concatenate document + trajectory into one sequence; (3) train with standard next-token loss, no special objectives, schedulers, or online rollouts.
Empirically, the authors show steadier gains than vanilla pre-training when data is constrained: the baseline plateaus as unique tokens are exhausted, while TPT keeps improving, especially on GSM8K and MATH, and remains competitive under abundant data as well. They also report consistent boosts in mid-training, including a public ~350k-sample SFT setting.